En geometría, las figuras tridimensionales como el cubo, la pirámide, el prisma y el cilindro son fundamentales para entender las formas y estructuras espaciales. Cada una de estas figuras tiene características específicas que las distinguen y les otorgan propiedades geométricas únicas.
A continuación, exploraremos en detalle cada una de estas figuras geométricas, describiendo sus características, fórmulas relacionadas y ejemplos prácticos donde se aplican. Comprender estas formas es esencial no solo para los estudios matemáticos, sino también para aplicaciones en arquitectura, ingeniería y diversas disciplinas científicas.
¿Qué es un cubo?
Un cubo es un poliedro regular compuesto por seis caras cuadradas de igual tamaño. Todas sus aristas tienen la misma longitud y forman ángulos rectos entre sí. El cubo es una de las cinco figuras conocidas como sólidos platónicos.
Caras: 6 caras cuadradas
Aristas: 12 aristas de igual longitud
Vértices: 8 vértices
La fórmula para calcular el volumen de un cubo es V = a³, donde a es la longitud de una arista. La fórmula para calcular el área superficial es A = 6a².
¿Qué es una pirámide?
Una pirámide es una figura tridimensional que tiene una base poligonal y caras triangulares que convergen en un solo punto llamado vértice. Las pirámides se clasifican según la forma de su base, pudiendo ser triangular, cuadrada, pentagonal, etc.
Base: Polígono (puede variar)
Caras laterales: Triangulares
Vértice: Un solo punto donde se unen las caras laterales
La fórmula para calcular el volumen de una pirámide es V = (1/3)Bh, donde B es el área de la base y h es la altura. El área superficial varía según la forma de la base y debe sumarse el área de las caras laterales.
¿Qué es un prisma?
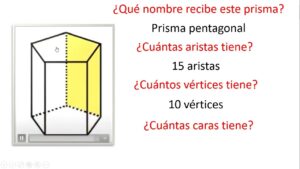
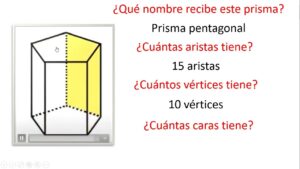
Un prisma es una figura tridimensional con dos bases paralelas e iguales y caras laterales rectangulares. Los prismas se clasifican según la forma de sus bases, que pueden ser triangulares, cuadradas, rectangulares, entre otras.
Bases: Dos polígonos paralelos e iguales
Caras laterales: Rectángulos
Aristas: Cantidad depende del tipo de base
La fórmula para calcular el volumen de un prisma es V = Bh, donde B es el área de la base y h es la altura. El área superficial se calcula sumando el área de todas las caras.
¿Qué es un cilindro?
Un cilindro es una figura tridimensional con dos bases circulares paralelas y una superficie lateral curva que conecta las bases. A menudo se compara con un prisma de bases circulares.
La fórmula para calcular el volumen de un cilindro es V = πr²h, donde r es el radio de la base y h es la altura. La fórmula para calcular el área superficial es A = 2πrh + 2πr².
Propiedades geométricas y fórmulas del volumen del cubo
El cubo, también conocido como hexaedro regular, es una de las figuras geométricas más importantes y estudiadas en geometría. Un cubo está formado por seis caras cuadradas, ocho vértices y doce aristas. Vamos a explorar sus propiedades geométricas y la fórmula para calcular su volumen.
Propiedades geométricas del cubo
El cubo tiene seis caras, todas ellas son cuadrados.
Posee doce aristas, y todas son de la misma longitud.
Cuenta con ocho vértices, donde se encuentran tres aristas en cada vértice.
Las diagonales de las caras del cubo son iguales en longitud.
Las diagonales del cubo atraviesan su centro y son iguales en longitud.
Estas propiedades hacen que el cubo tenga una simetría notable y sea un ejemplo perfecto de un sólido platónico.
Cálculo del volumen del cubo
El volumen de un cubo se puede calcular utilizando la longitud de una de sus aristas. La fórmula para encontrar el volumen V de un cubo es:
V = a³
donde a es la longitud de una arista del cubo. Por ejemplo, si la longitud de la arista es de 3 cm, el volumen del cubo sería:
V = 3 cm × 3 cm × 3 cm = 27 cm³
Ejemplos concretos
Consideremos algunos ejemplos para ilustrar mejor cómo se aplica esta fórmula:
Si un cubo tiene una arista de 5 cm, su volumen será:
V = 5 cm × 5 cm × 5 cm = 125 cm³
Para un cubo con una arista de 10 cm, el volumen será:
V = 10 cm × 10 cm × 10 cm = 1000 cm³
Consejo práctico
Cuando trabajes con cubos en problemas de matemáticas o geometría, asegúrate de medir la longitud de la arista con precisión. Una pequeña diferencia en la medida puede llevar a un error significativo en el cálculo del volumen. Además, recuerda que todas las aristas de un cubo son iguales, lo que simplifica mucho el proceso de cálculo.
Aplicaciones del cubo en la vida real
El cubo no solo es una figura teórica en matemáticas, sino que tiene múltiples aplicaciones en el mundo real. Por ejemplo:
En arquitectura, los cubos se utilizan en el diseño de edificios y estructuras.
En almacenamiento, muchas cajas y contenedores tienen forma de cubo debido a su eficiencia en el uso del espacio.
En tecnología, los cubos se emplean en la representación de datos tridimensionales y en la modelización 3D.
Aplicaciones prácticas de la pirámide en arquitectura y diseño
La pirámide es una figura geométrica que ha capturado la imaginación de arquitectos y diseñadores a lo largo de la historia. Su estructura no solo es estéticamente atractiva, sino que también ofrece múltiples ventajas en términos de estabilidad y funcionalidad. A continuación, exploraremos algunas de las aplicaciones más destacadas de las pirámides en el campo de la arquitectura y el diseño.
1. Estabilidad estructural
Una de las principales razones por las que las pirámides han sido utilizadas en la arquitectura es su estabilidad. La forma piramidal distribuye el peso de manera uniforme, lo que minimiza el riesgo de colapso. Un claro ejemplo de esta aplicación son las pirámides de Egipto, que han resistido el paso del tiempo durante miles de años.
2. Eficiencia en el uso del espacio
Las pirámides permiten un uso eficiente del espacio. Al tener una base ancha que se estrecha hacia la cima, se pueden construir estructuras que ocupan menos espacio en el suelo mientras ofrecen un volumen considerable. Esto es especialmente útil en áreas urbanas donde el terreno es limitado.
Ejemplo: La Pirámide del Louvre
La Pirámide del Louvre en París es un excelente ejemplo de cómo se puede utilizar una pirámide para maximizar el uso del espacio. La estructura sirve como una entrada que permite la circulación eficiente de los visitantes, al mismo tiempo que se integra visualmente con el entorno histórico del museo.
3. Innovación en diseño
Más allá de su funcionalidad, las pirámides también ofrecen oportunidades para la innovación en el diseño. Su forma distintiva puede ser utilizada para crear edificios que se destacan visualmente y que capturan la atención de las personas.
Ejemplo: El Luxor Hotel en Las Vegas
El Luxor Hotel en Las Vegas es un ejemplo moderno de cómo la forma piramidal puede ser utilizada para crear un diseño innovador. La estructura no solo es un hotel, sino también un símbolo icónico de la ciudad, atrayendo a miles de turistas cada año.
4. Eficiencia energética
La forma piramidal también puede contribuir a la eficiencia energética de un edificio. La inclinación de las paredes permite una mejor circulación del aire y puede reducir la necesidad de climatización. Además, la orientación de las pirámides puede ser aprovechada para maximizar la captación de energía solar.
Considera la orientación de la pirámide para aprovechar al máximo la luz solar.
Utiliza materiales de construcción que complementen la eficiencia energética de la forma piramidal.
5. Resistencia a condiciones climáticas
Las pirámides son conocidas por su resistencia a condiciones climáticas adversas. La estructura inclinada permite que el viento pase fácilmente alrededor del edificio, y la base ancha proporciona una sólida fundación capaz de soportar condiciones extremas.
Ejemplo: Templos Mayas
Los templos mayas, como el Templo de Kukulkán en Chichén Itzá, son ejemplos históricos de cómo las pirámides pueden resistir condiciones climáticas severas. Estas estructuras han sobrevivido a huracanes y terremotos durante siglos.
Las aplicaciones de las pirámides en arquitectura y diseño son variadas y ofrecen múltiples beneficios, desde la estabilidad estructural hasta la eficiencia energética. Al considerar el uso de esta figura geométrica, los diseñadores y arquitectos pueden crear estructuras que no solo sean visualmente atractivas, sino también altamente funcionales y sostenibles.
Preguntas frecuentes
¿Qué es un cubo en geometría?
Un cubo es un poliedro de seis caras cuadradas iguales y doce aristas.
¿Qué es una pirámide en geometría?
Una pirámide es un poliedro con una base poligonal y caras laterales triangulares que convergen en un vértice.
¿Qué es un prisma en geometría?
Un prisma es un poliedro con dos caras iguales y paralelas (llamadas bases) y caras laterales que son paralelogramos.
¿Qué es un cilindro en geometría?
Un cilindro es un cuerpo geométrico con dos bases circulares iguales y una superficie lateral curva.
A continuación se presentan algunos puntos clave sobre los cuerpos geométricos:
Los cuerpos geométricos tienen dimensiones como longitud, anchura y altura.
El volumen de un cubo se calcula elevando al cubo la longitud de una de sus aristas.
La fórmula para calcular el volumen de una pirámide es V = (1/3) * Area de la base * Altura.
El prisma tiene la misma sección transversal a lo largo de toda su longitud.
El cilindro tiene dos bases circulares iguales y su fórmula de volumen es V = π * radio al cuadrado * altura.
Si te interesa aprender más sobre geometría y sus aplicaciones, déjanos tus comentarios y revisa otros artículos relacionados en nuestra web.
